How to Calculate the KL Divergence for Machine Learning

Last Updated on November 1, 2019

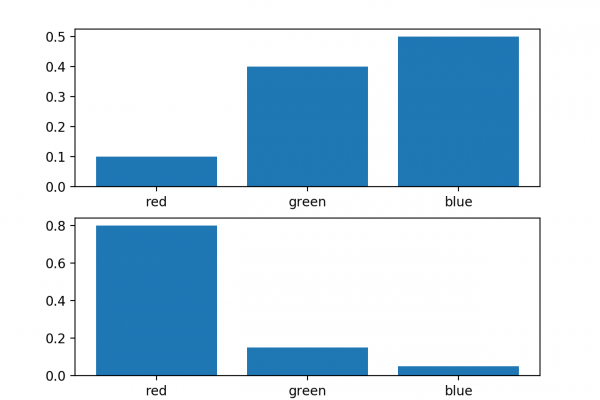
It is often desirable to quantify the difference between probability distributions for a given random variable.

This occurs frequently in machine learning, when we may be interested in calculating the difference between an actual and observed probability distribution.

This can be achieved using techniques from information theory, such as the Kullback-Leibler Divergence (KL divergence), or relative entropy, and the Jensen-Shannon Divergence that provides a normalized and symmetrical version of the KL divergence. These scoring methods can be used as shortcuts in the calculation of other widely used methods, such as mutual information for feature selection prior to modeling, and cross-entropy used as a loss function for many different classifier models.

In this post, you will discover how to calculate the divergence between probability distributions.

After reading this post, you will know:

• Statistical distance is the general idea of calculating the difference between statistical objects like different probability distributions for a random variable.
• Kullback-Leibler divergence calculates a score that measures the divergence of one probability distribution from another.
• Jensen-Shannon divergence extends KL divergence to calculate a symmetrical score and distance measure of one probability distribution from another.

Kick-start your project with
To finish reading, please visit source site