A Gentle Introduction to Expectation-Maximization (EM Algorithm)

Last Updated on August 28, 2020

Maximum likelihood estimation is an approach to density estimation for a dataset by searching across probability distributions and their parameters.

It is a general and effective approach that underlies many machine learning algorithms, although it requires that the training dataset is complete, e.g. all relevant interacting random variables are present. Maximum likelihood becomes intractable if there are variables that interact with those in the dataset but were hidden or not observed, so-called latent variables.

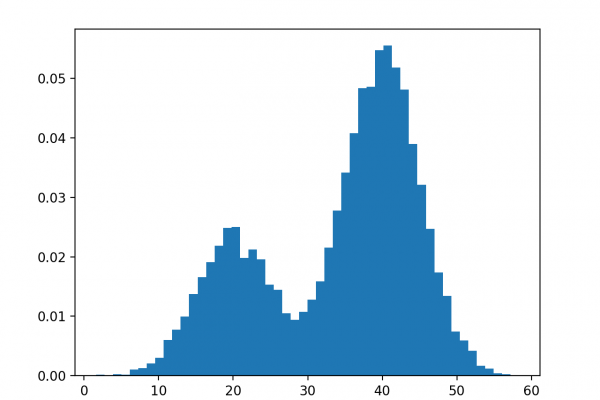
The expectation-maximization algorithm is an approach for performing maximum likelihood estimation in the presence of latent variables. It does this by first estimating the values for the latent variables, then optimizing the model, then repeating these two steps until convergence. It is an effective and general approach and is most commonly used for density estimation with missing data, such as clustering algorithms like the Gaussian Mixture Model.

In this post, you will discover the expectation-maximization algorithm.

After reading this post, you will know:

• Maximum likelihood estimation is challenging on data in the presence of latent variables.
• Expectation maximization provides an iterative solution to maximum likelihood estimation with latent variables.
• Gaussian mixture models are an approach to density estimation
  To finish reading, please visit source site